Binary search

#

Binary search is a better version of Linear search. Here, rather than checking each element one by one, we split the data structure in two halves and then compare our target with the middle element. But this comparison only makes sense if the data structure is either sorted in an ascending or a descending manner. Therefore -

The array must be sorted for binary search to work.

Now lets try to see how it works step by step -

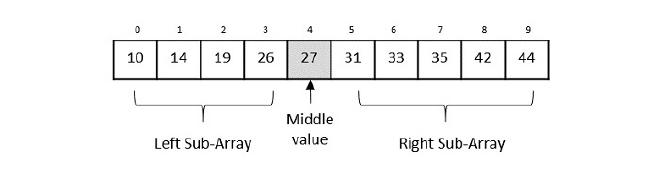
1. Let’s take an array for our example and try to understand what happens in Binary search. Let us suppose our target is 42.

2. First up, we have our starting index as 0 and our last index as n-1 (where n = total length of the array) and this is always the case with all arrays. This is where our search should happen.

3. Finding the mid value becomes easy now with the formula $$ (start+end)/2 $$ here this will be $$ (0+9)/2 = 4.5 = 4 $$(we will keep all parameters as int to make finding the middle easily.)

4. Now we can find the middle-most element as 27. Since array is sorted in an ascending order, we can see that our target is greater than the middle element hence we only need to search the right sub-array which contains elements larger than the center element

5. Now comes an important step. We have to change the start and end positions.

   • In case our target>middle element, we change the start as middle + 1
   • In case our target<middle element, we change the end to middle - 1
   • Otherwise target=middle In our case, we have target>middle, meaning we only have to search the right sub-tree so we need to change the start to middle+1, which will become, 4+1= 5. So now we will search from 5 to end (end is still the same, i.e. 9)

6. Repeat Step 3 and our middle index now becomes 7. The element at 7 is 35, i.e. target>middle element so start = middle +1. Now our start becomes 8. That means we will search from 8 to 9.

7. Repeat Step 3 and our middle index now becomes 8. This time when comparing the element at 8, we observe it is our target i.e. 42.

Similarly, we simply change the end to middle-1 in case we want to check the left sub-array and repeat the same process.

The code for the same in Python-

def binary_search(arr, x):
	start = 0
	end = len(arr) - 1
	 
	while (start <= end):
		mid = start + (end-start)/2
		if arr[mid] > x:
			end = mid - 1
		elif arr[mid] <x:
			start = mid + 1
		else:
			return mid
	return -1 #incase the target entered is not inside our array
	
arr = [10,14,19,26,27,31,33,35,42,44]
x = 42
result = binary_search(arr,x)

if result != -1:
	print("Element at index", result)
else:
	print("Element entered is not present in the array.")
	
	

Oops

#

Did you notice the formula I used to find the middle value in the above example? Well, If we think about it, calculating our middle index with the previous formula can be a bit tricky sometimes. Especially when both our start and end indices have very large values. By large, I mean large enough that sometimes, they can not be contained within certain data types (as every data type has a range. In C++, the range of int is -2,147,483,648 to 2,147,483,647). Now we may not reach these number of indices but our code is supposed to work for ALL kinds of data and there is a very simple way to avoid this problem.

Our problem occurs because we are supposedly adding 2 very large numbers whose sum can not be fit into our data type. But if we use the formula, $$ Mid = start + (end-start)/2$$ we are subtracting two huge numbers, dividing it by 2 and then adding a huge number which will not overflow our datatype! Also if simplify this formula, it’s basically a complicated way of writing the same thing but here, this gets our job done and not the simplified version so it’s better to use this instead of the previous one!

All the topics I’ll be covering in this blog are more or less related to the curriculum of my college. I might miss on some topics related to this topic. Feel free to reach out and let me know if I should add something else!